教师导得更智慧学生学得更生动课堂教学更高效
------天津市扶轮中学教师教案、学案精选
《确定二次函数的解析式》(教案)
一、教学重点:已知二次函数图象上一个点的坐标或三个点的坐标,分别求二次函数
y=ax2、y=ax2+bx+c的关系式。
二、教学难点:已知图象上三个点坐标求二次函数的关系式。
1.使学生掌握用待定系数法由已知图象上一个点的坐标求二次函数y=ax2的关系式。
2.使学生掌握用待定系数法由已知图象上三个点的坐标求二次函数y=ax2+bx+c的关系式。
3.让学生体验二次函数的函数关系式的应用,提高学生用数学意识。
三、教学过程:
(一)创设问题情境
如图,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶。它的拱宽AB为4m,拱高CO为0.8m。施工前要先制造建筑模板,怎样画出模板的轮廓线呢?
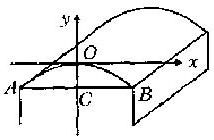
分析:为了画出符合要求的模板,通常要先建立适当的直角坐标系,再写出函数关系式,然后根据这个关系式进行计算,放样画图。
如图所示,以AB的垂直平分线为y轴,以过点O的y轴的垂线为x轴,建立直角坐标系。这时,屋顶的横截面所成抛物线的顶点在原点,对称轴是y轴,开口向下,所以可设它的函数关系式为: y=ax2 (a<0)(1)
因为y轴垂直平分AB,并交AB于点C,所以CB=AB/2=2(cm),又CO=0.8m,所以点B的坐标为(2,-0.8)。
因为点B在抛物线上,将它的坐标代入(1),得 -0. 8=a×22 所以a=-0.2
因此,所求函数关系式是y=-0.2x2。
请同学们根据这个函数关系式,画出模板的轮廓线。
(二)引申拓展
问题1:能不能以A点为原点,AB所在直线为x轴,过点A的x轴的垂线为y轴,建立直角坐标系?
让学生了解建立直角坐标系的方法不是唯一的,以A点为原点,AB所在的直线为x轴,过点A的x轴的垂线为y轴,建立直角坐标系也是可行的。
问题2,若以A点为原点,AB所在直线为x轴,过点A的x轴的垂直为y轴,建立直角坐标系,你能求出其函数关系式吗?
分析:按此方法建立直角坐标系,则A点坐标为(0,0),B点坐标为(4,0),OC所在直线为抛物线的对称轴,所以有AC=CB,AC=2m,O点坐标为(2,0.8)。即把问题转化为:已知抛物线过(0,0)、(4,0)、(2,0.8)三点,求这个二次函数的关系式。
二次函数的一般形式是y=ax2+bx+c,求这个二次函数的关系式,跟以前学过求一次函数的关系式一样,关键是确定a、b、c,已知三点在抛物线上,所以它的坐标必须适合所求的函数关系式;可列出三个方程,解此方程组,求出三个待定系数。
解:设所求的二次函数关系式为y=ax2+bx+c
因为OC所在直线为抛物线的对称轴,所以有AC=CB,AC=2m,拱高OC=0.8m,所以O点坐标为(2,0.8),A点坐标为(0,0),B点坐标为(4,0)。
由已知,函数的图象过(0,0),可得c=0,又由于其图象过(2,0.8)、(4,0),可得到4a+2b=0.816a+4b=0解这个方程组,得a=-■b=■所以,所求的二次函数的关系式为y=-■x2+■x。
问题3:根据这个函数关系式,画出模板的轮廓线,其图象是否与前面所画图象相同?
问题4:比较两种建立直角坐标系的方式,你认为哪种建立直角坐标系方式能使解决问题来得更简便?为什么?
(第一种建立直角坐标系能使解决问题来得更简便,这是因为所设函数关系式待定系数少,所求出的函数关系式简单,相应地作图象也容易)
(三)课堂练习:学案(二)1、2。
(四)综合运用
例1.如图所示,求二次函数的关系式。
分析:观察图象可知,A点坐标是(8,0),C点坐标为(0,4)。从图中可知对称轴是直线x=3,由于抛物线是关于对称轴的轴对称图形,所以此抛物线在x轴上的另一交点B的坐标是(-2,0),问题转化为已知三点求函数关系式。
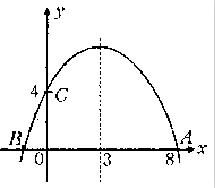
解:观察图象可知,A、C两点的坐标分别是(8,0)、(0,4),对称轴是直线x=3。因为对称轴是直线x=3,所以B点坐标为(-2,0)。
设所求二次函数为y=ax2+bx+c,由已知,这个图象经过点(0,4),可以得到c=4,又由于其图象过(8,0)、(-2,0)两点,可以得到64a+8b=-44a-2b=-4解这个方程组,得a=-■b=■所以,所求二次函数的关系式是y=-■x2+■x+4
练习:学案(二)3、4。
(五)小结
二次函数的关系式有几种形式,函数的关系式y=ax2+bx+c就是其中一种常见的形式。二次函数关系式的确定,关键在于求出三个待定系数a、b、c,由于已知三点坐标必须适合所求的函数关系式,故可列出三个方程,求出三个待定系数。
(六)作业
1.二次函数的图象的顶点在原点,且过点(2,4),求这个二次函数的关系式。
2.若二次函数的图象经过A(0,0),B(-1,-11),C(1,9)三点,求这个二次函数的解析式。
3.如果抛物线y=ax2+bx+c经过点(-1,12),(0,5)和(2,-3),求a+b+c的值。
4.已知二次函数y=ax2+bx+c的图象如图所示,求这个二次函数的关系式;
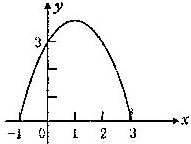
5.二次函数y=ax2+bx+c与x轴的两交点的横坐标是-1/2,3/2,与y轴交点的纵坐标是-5,求这个二次函数的关系式。
(七)反思
1.得出结论:凡是能用“顶点式”确定的,一定可用“一般式”确定,进一步明确两种表达式只是形式的不同和没有本质的区别;在做题时,不仅会使用已知条件,同时要养成挖掘和运用隐含条件的习惯。
2.在知识运用部分采用猜想、比较、方法选择等方法引导学生探究问题,从而大大地提高学生分析问题、解决问题的能力。
《确定二次函数的解析式》(学案)
一、学习目标
1.会利用待定系数法求二次函数,并能正确地求出函数关系式。
2.能选择合理简便的方法求函数关系式。
二、学习重点:能选择合理简便的方法求函数关系式。
三、学习难点:正确地求出函数关系式。
四、 学习过程:
能根据题目所提供的条件灵活选用二次函数表达式的类型,体会待定系数法的思想;经常不能准确地求出函数的表达式,是因为运算能力较差。先自主探究,有困难的话,可以请求同学或教师帮助。
(一) 知识链接
1.我们已经了解了二次函数的图象和性质,那么如何确定二次函数的表达式呢?我们先来回顾确定一次函数或反比例函数的表达式的步骤是什么?
2.y与x成正比例,其图象过点P(■,1),则函数关系式为
。
3.一次函数y =kx+b的图象过(5,-2),(2,1),求函数关系式。
(二)探究新知
例1:已知二次函数的图象经过(0,2),(1,0)和(-2,3),求这个函数的表达式。
练习 :1.已知一个二次函数的图象经过(-1,10),(1,4),(2,7),求这个二次函数的解析式。
2. 已知一个二次函数的图象经过(1,2)、(3,0)、(-2,20)三点,求函数的表达式。
例 2:已知二次函数的顶点坐标为(-1,-6),并且经过(2,3),求这个二次函数的表达式。
练习:1.已知抛物线的顶点坐标是(-1,-2),且图象经过点(1,10),求函数关系式。
2.已知抛物线的顶点坐标是(1,-2),且图象经过点(3,6),求函数关系式。
(三) 小结
本节课所学的知识点:如何求二次函数的表达式?
(1)设出二次函数相应的表达式
(2)列方程(组)求待定系数
(3)写出二次函数的表达式
《分子热运动》(教案)
教学目标
1.知识与技能
☆知道物质是由分子组成的,一切物质的分子都在不停地做无规则的运动。
☆能识别扩散现象,并能用分子热运动的观点进行解释。
☆知道分子热运动的快慢与温度的关系。
☆知道分子之间存在相互作用力。
2.过程与方法
☆通过演示实验,说明一切物质的分子都在不停地做无规则的运动。
☆通过演示实验,使学生推测出物体温度越高,热运动越剧烈。
☆通过演示实验以及与弹簧的弹力类比,使学生了解分子之间既存在斥力又存在引力。
3.情感态度与价值观
☆用演示实验激发学生的学习兴趣,通过交流讨论培养学生的合作意识和能力。
教学重点与难点
分子的热运动是本节的重点;通过直接感知的现象,推测无法直接感知的事实是本节的难点。
教学课时:1时
教学过程
引入新课
我们生活在物质世界中,我们的周围充满着物质:水、空气、石头、金属、动物、植物等都是物质。而对于“物质是怎样构成的”这一古老课题,很早就有过种种猜测,有的主张万物之源是“气”;有的主张万物之源是“火”。公元前5世纪,墨子提出物质的最小单位是“端”;公元前4世纪,古希腊德漠克利特认为,宇宙万物是由大小和质量不同的、不可分的、运动不息的原子组成。此后经过近2000年的探索,直到17世纪末,人们才科学地认识到物质是由分子组成的。
进行新课
(1)分子和分子运动
①物质是由分子组成的,分子是极小的微粒。如果把分子看作球形,它的直径约10-10米,这是一个极小的长度,不仅肉眼看不到,即使用现代显微镜也看不清。由于分子极小,所以物体含分子数目大得惊人。通常情况下,1立方厘米空气里大约有2.7×1019个分子,如果每秒数100亿个,要数完这个数,也得用80多年。
②构成物质的分子永不停息地运动着。由于分子太小,目前尚无法直接观察分子的行为,但我们可以从宏观的实验现象来判断分子的行为。
演示实验一:花露水扩散
演示实验二:二氧化氮气体扩散(视频观看)
出示事先装有二氧化氮(或溴气)气体的广口瓶,说明瓶内红棕色的气体是二氧化氮。再出示一只空广口瓶,其实瓶内装满了空气。将装有二氧化氮的瓶子向空瓶倾倒,这时看到红棕色气体流入空瓶,并沉到瓶底。此现象说明二氧化氮的密度大于空气的密度。
另取一只空瓶,将其倒扣在装有二氧化氮气体的瓶子上。这时,要强调装有密度较大的二氧化氮气体的瓶子在下,装有空气的瓶子在上,抽掉玻璃隔板,二氧化氮气体不会流进空气瓶内。现在抽掉隔板,没有出现二氧化氮气体流动的现象,停一会儿再来观察瓶内出现的现象。
演示实验三:红墨水扩散
在等候期间,组织学生做红墨水扩散实验:同学们课桌上的烧杯里盛有清水,大家不要振动桌子,保持清水平静。请大家向清水里慢慢地滴入一滴红墨水,观察墨水的变化情况。滴入的墨水下沉,在清水中留下清晰的墨迹。过一段时间,墨迹的轮廓变模糊,墨迹变淡,周围的水色变红。
组织学生观察前面已做的气体扩散实验:此时空气瓶出现了红棕色,下面红棕色的二氧化氮瓶中颜色变淡。实验现象表明,二氧化氮气体进入了空气,空气进入了二氧化氮气体中。像这样,不同的物体在互相接触时,彼此进入对方的现象,叫做扩散。
扩散现象也可以发生在液体之间。请大家再观察一下刚才滴入墨水的清水,已经没有明显的墨迹,整杯水都变红了,说明墨水和水也发生了扩散。为了说明液体的扩散现象,我们再来看段视频(硫酸铜溶液和水的扩散)。现在我们看到无色的清水和蓝色的硫酸铜溶液之间有明显的界面,要观察到扩散现象需要较长的时间。为了节省课堂时间,出示提前二天、四天、六天做的实验样本。这些实验告诉我们,静放的时间越长,界面变得越模糊不清,彼此进入对方越深。
固体之间也会发生扩散现象。将铅片和金片紧压在一起,放置5年后再将它们分开,可以看到它们相互渗入约1毫米。其实在日常生活中,我们也可观察到固体的扩散。有的煤矿石原本是石炭岩,由于长期地跟煤挤压在一起,它的内部也变黑了。
大量事实说明,气体、液体、固体都有扩散现象,即使在日常生活中,大家也能找到许多事例。例如某同学搽点清凉油,周围同学就能闻到清凉油味。
扩散现象表明,一切物体的分子都在不停地做无规则的运动。只有分子不停地运动,才能相互进入对方。同时也说明,分子不是紧密地挤在一起,而是彼此间存有间隙。
(2)分子间的作用力
固体、液体的分子都在不停地做无规则运动,且分子间又有间隙,为什么分子不会飞散开,反而聚合在一起呢?引导学生猜想,这可能是因为分子间存在着吸引力。这个猜想是否正确呢?需要我们用实验来证实。
演示实验:分子引力实验
出示演示分子引力的两个铅圆柱。随意将它们对在一起,这时两铅块并没有表现出吸引力。实验似乎得到分子间没有引力的结果,但是我们不要轻易地放弃我们的猜想,应进一步分析原因。大家都知道,磁铁能够吸引铁钉(边讲边演示),但把铁钉远离磁铁,这时磁铁不能吸起铁钉(演示),这是为什么?(距离太远)。刚才两铅块没有表现出吸引力,是不是也是因为分子间的距离不够近呢?那么,我们让两铅块靠得更近些(再做实验时,用小刀将两铅块表面刮光亮,然后用力将两铅块挤压在一起)。
实验结果是两铅块能吸引在一起,并能负重达500克以上。这表明只有在分子靠得很近时,分子之间的吸引力才能表现出来。一般分子在距离小于10-9米时,才能表现出引力。
在实际生产中,人们早就利用分子间的吸引力来进行金属焊接了。一般焊接是靠溶化金属,从而使分子间的距离足够近,金属冷却后就焊接到一起。近代还有爆破焊接技术,它是将金属表面清洁后靠在一起,然后靠爆炸产生的巨大压力,将两金属压接在一起。
液体分子之间也存在吸引力。课本图16-1-7的小实验就说明液体分子间的吸引力(视频观看)。
实验证实了我们关于分子引力的猜想。我们再进一步思考,又会发现新的矛盾:分子之间既有间隙又有引力,这两者是矛盾的。分子相互吸引,最终应该相互靠紧,而不应该有间隙。既然分子间有间隙,物体应该很容易压缩,但事实却是固体、液体极难压缩。事实表明我们对分子的认识还不够全面,还有没认识到的方面。
原来,分子之间还存在斥力。分子之间既有引力,又有斥力,会不会两种力总是相互抵消呢?当然不会,只有在特定的距离r0时,分子间的引力等于斥力,这个距离r0就是通常分子间隙的距离,大约是10-10米。当分子距离小于r0时,斥力和引力都增大,但斥力增大得快,分子间表现为斥力。当分子间距离增大时,斥力和引力都减小,但斥力减小得更快,分子间表现为引力。当分子距离再增大,分子引力继续减小,当分子距离大于10r0时,分子间的作用力将变得十分微弱,可以忽略了。
有了对分子间存在斥力的认识,前面所说的矛盾也就迎刃而解了。
小结
通过实验和思考,我们已经对分子和分子的运动有了初步认识,现在我们共同回顾一下,看看我们已经有了哪些认识。
1.物质是由分子组成的,分子是构成物质的微粒,直径大约是10-10米。
2.分子永不停息地无规则运动着。
3.分子之间有间隙。
4.分子之间存在作用力,相互作用力有两种,即引力和斥力。
以上几点是分子动理论的基本要点。利用这些要点,能够解释很多热现象。
作业:练习册
《分子热运动》(学案)
【学习目标】
1.知道物质是由分子组成的,一切物质的分子都在不停地做无规则的运动。
2.能识别扩散现象,并能用分子热运动的观点进行解释。
3.知道分子热运动的快慢与温度的关系。
4.知道分子之间存在相互作用力。☆通过演示实验说明一切物质的分子都在不停地做无规则的运动。
【重点难点】分子的热运动
【实验器材】烧杯、热水、冷水、铅块、红墨水
【学习过程】
知识回顾:
1. 分子是保持 的最小微粒。
2. 分子直径大约为 米,一般我们用 来衡量。
新课讲授:
一、 物质是由 组成的。
二、 扩散:
实验一:房间内喷空气清新剂
实验二:二氧化氮扩散
——————观察有什么现象出现
实验三:红墨水在清水中扩散
1. 物质在相互 时,彼此进入对方的现象叫扩散。
2. 都可以发生扩散现象。
3.扩散现象表明:一切物质的分子都在不停地做 ,分子间有 。
4.影响扩散快慢的因素:
探究实验:影响扩散快慢的因素。
实验器材:两只相同的烧杯、热水、冷水、红墨水
讨论并用所给器材来验证
结论:影响扩散快慢的主要因素是
, 越高,分子运动越快,扩散越快。除了温度, 也会影响扩散的快慢。
三、 分子间作用力
1. 分子间存在相互作用的 。
2.分子间存在相互作用的 。
3.①r=r0时,引力 斥力(r0=10-10m)。
②r<r0时,引力和斥力都增大,但是斥力增大得快,引力 斥力,分子间表现为 。
③r>r0时,引力和斥力都减小,但是斥力减小得快,引力 斥力,分子间表现为 。
④r>10r0时,分子间作用力变得十分微弱,可以忽略不计。
四、 分子动理论
1.物质是由 成的。
2.一切物质的分子都在不停地 。
3.分子间有 。
4.分子间存在相互作用的 和 。
能力提升:
1.“花气袭人知骤暖,鹊声穿树喜新晴”,这是南宋诗人陆游《村居书喜》中的两句诗,写春晴天暖、鸟语花香的山村美景。对于前一句,从物理学的角度可以理解为:花朵分泌的芳香油分子_______________加快,说明当时周边气温突然_______。
2.下列有关生活现象中,不能用分子动理论来解释的是 ( )
A.阳光下,湿衣服很快干了。
B.轻轻地弹一下,衣服上的灰尘“跑”了。
C.随风飘来了醉人的花香。
D.衣柜中的樟脑丸过一段时间消失了。
3.判断对错:
扩散表明,物体的分子永不停息地做无规则运动。( )
铁丝不易被拉断是分子间存在着引力的原因。( )
分子间有时有引力,有时有斥力。 ( )
固体很硬,所以固体之间不会发生扩散。 ( )
4.水很难被压缩,其原因是( )
A.水分子之间没有空隙。
B.水分子之间有引力。
C.水分子之间有斥力。
D.水分子在不停地运动。
5.在下列现象中,能说明分子不停地做无规则运动的现象是( )
A.在皮肤上搽点酒精,立即就能闻到酒精的味道。
B.鱼苗池中的小鱼在不停地游动。
C.教室里大扫除时,灰尘满屋飞扬。
D.落叶在河水中顺流而下。
6.一滴红墨水滴入一杯清水中,过一段时间后,整杯水都变红了,下列说法中正确的是( )
A.如果是0 ℃的水,就不会发生这种现象。
B.这叫扩散现象,它只能发生在液体中。
C.清水的温度越高,扩散进行得越快。
D.这叫扩散现象,它说明分子是在永不停息地运动着。
7.把两块光滑的玻璃贴紧,它们不能吸在一起,原因是( )
A.两块玻璃分子间存在斥力。
B.两块玻璃的分子间距离太大。
C.玻璃分子间隔太小,不能形成扩散。
D.玻璃分子运动缓慢。
8.腌制咸菜时,咸菜很长时间才会咸,煮茶叶蛋时茶叶蛋一会儿就咸了,为什么?
《牛顿第三定律》导学案
★学习目标
⑴知道力的作用是相互的,理解作用力和反作用力的概念。
⑵理解牛顿第三定律,会运用牛顿第三定律解释生活中的有关现象。
⑶能够区分平衡力与相互作用力的异同点。
★学习重点
⑴ 探究作用力与反作用力之间的关系,掌握探究的基本方法。
⑵理解牛顿第三定律,并用它分析实际问题。
(3)相互作用力与一对平衡力的区别。
★学习难点
区别平衡力与作用力和反作用力。
★学法指导
合作探究、交流讨论、自主归纳。
★学习过程
【任务一】作用力和反作用力
学生活动:1. 力的定义是什么?如何理解相互作用,举例说明?
2.(看教材81页图4.5-1和4.5-3),总结什么是作用力和反作用力。
学生总结:作用力和反作用力
一个物体对另一个物体施加了力,后一物体一定同时对前一物体也施加了力;物体间相互作用的这一对力,通常把其中一个力叫做作用力,另一个力叫做反作用力。
【任务二】探究作用力与反作用力的关系
学生活动
1.想一想:研究力,我们从哪几个要素入手?
研究相互作用力的方向: 。
2.猜想:根据原有的知识和生活经验,作用力与反作用力有哪些关系和特点?
(1)大小特点,我的猜想是: _____。
(2)方向特点, 我的猜想是:_____。
(3作用点特点,我的猜想是:_____。
3.分组实验探究:利用两只弹簧秤探究物体间相互作用力的大小关系。
实验指导:使用弹簧秤时的注意事项
(1)使用弹簧秤前,先进行______,观察_______及__________。
(2)拉伸弹簧秤时不能__________。
(3)指针应与弹簧秤外壁保持_______,不能有摩擦。
(4)测量相互作用力时,应保证两只弹簧秤在同一______上。
探究1 静止的物体间的相互作用力
探究结果: (1)大小特点 (2)变化情况
探究2 运动物体间的相互作用力
探究结果:(1)大小特点 (2)变化情况
实验后学生总结:
根据探究实验的结果,我的结论是作用力与反作用力的关系为__________。
4 .观看视频:用传感器探究作用力与反作用力的关系。
通过现代化实验,我们可以得出:作用力与反作用力的关系是________。
【任务三】牛顿第三定律
师生互动:共同总结牛顿第三定律的内容、表达式及作用力与反作用力的特点。
1.内容:两个物体之间的作用力和反作用力总是大小________,方向_______,作用在_______直线上。
2. 表达式:
3.作用力与反作用力的特点:_______________________________________________________________。
观看视频:生活中的牛顿第三定律:火箭升空、足球比赛、斯诺克比赛、小品卖拐。
学生活动:列举生活和生产中应用牛顿第三定律的实例,并加以分析。
【任务四】相互作用力和一对平衡力的区别与联系
学生活动:做一做
如图所示,在天花板上用轻质绳悬挂一只电灯。
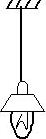
(1 )试在图中画出灯受到的重力G 、绳子对灯的拉力F1 、灯对绳子的拉力F2 、天花板对绳子的拉力F3 、绳子对天花板的拉力 F4五个力的示意图。
(2)试指出:这些力中有几对相互作用力和几对平衡力?分别是哪些?
相互作用力______; 平衡力____________。
小组讨论:平衡力与相互作用力的区别与联系,并完成下表。
【课堂反馈】
1. 以卵击石,蛋碎石全,为什么?
2 .一匹马拉着车在路上走,试分析下列情况下马对车的拉力和车对马的拉力大小关系:
A.车陷进泥潭里,马没有拉动车。
B.马拉着车在马路上匀速前进时。
C.马拉着车在马路上加速前进时。
D.到达地点它们要停下来时。
根据以上各种情况,我总结的规律是______________________________。
【总结提升】为什么相互作用力如此“简单”的关系能被称之为定律呢?
【拓展作业】
广泛收集有关牛顿第三定律应用的事例,加以分析,以小组为单位整理,以小论文、手抄报、网页、演示文稿等方式提交。
【达标检测】
1 .在水平粗糙地面上滑行的木块与地球之间的相互作用力有( )对
A.一对
B.两对
C.三对
D.四对
2.下列叙述中正确的是( )
A.作用力与反作用力一定是同种性质的力。
B.作用力与反作用力总是同时产生,同时消失。
C.作用力与反作用力有时可以是平衡力。
D.作用力与反作用力方向一定是相同的。
3. 手托着一木块,有静止开始向上减速运动,手对木块的支持力应该是( )
A.小于木块对手的压力。
B. 等于木块对手的压力。
C.大于木块对手的压力。
D.小于木块所受的重力。
4.春天,河边上的湿地很松软,人在湿地上行走时容易下陷,在人下陷时( )
A.人对湿地地面的压力就是他所受的重力。
B.人对湿地地面的压力大于湿地地面对他的支持力。
C.人对湿地地面的压力等于湿地地面对他的支持力。
D.人对湿地地面的压力小于湿地地面对他的支持力。
5.下列说法正确的是( )
A.走路时,只有地对脚的作用力大于脚蹬地的力时,人才能往前走。
B.走路时,地对脚的作用力与脚蹬地的力总是大小相等、方向相反的。
C.物体A静止在物体B上,A的质量是B的质量的10倍,则A对B的作用力大于B对A的作用力。
D.以卵击石,石头没有损伤而鸡蛋破了,是因为鸡蛋对石头的作用力小于石头对鸡蛋的作用力。
6.(2011·高考浙江卷)如图4-5-11所示,甲、乙两人在冰面上“拔河”,两人中间位置处有一分界线,约定先使对方过分界线者为赢。若绳子质量不计,冰面可看成光滑,则下列说法正确的是( )
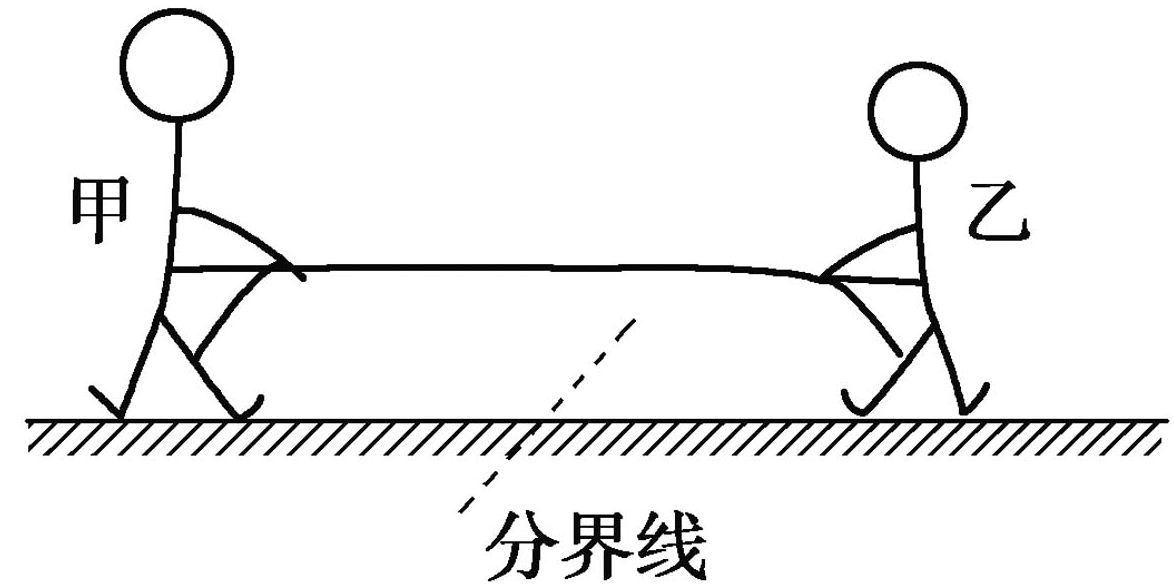
A.甲对绳的拉力与绳对甲的拉力是一对平衡力。
B.甲对绳的拉力与乙对绳的拉力是作用力与反作用力。
C.若甲的质量比乙大,则甲能赢得“拔河”比赛的胜利。
D.若乙收绳的速度比甲快,则乙能赢得“拔河”比赛的胜利。