河北区昆纬路第一小学 崔建哲
应用题教学是小学数学教学的重要内容,其中分数应用题是小学生学习的一个难点。这就要求教师要以学生的主体发展为核心,引导学生学会通过画线段图解答分数应用题的方法,促使其主动参与实践活动,培养他们的创新意识及创新精神,加快他们创新思维的发展。
分数应用题教学中,教师采用画线段图的方法,可以把比较抽象的数量关系形象地描绘出来,还可以直观地揭示出条件与条件、条件与问题之间的关系,把数转化为形,启发学生的解题思路,激活学生的再造性想象,充分发挥形象思维与抽象思维的互助、互补、相辅相成的作用,同时达到帮助学生找到解题方法的目标,以提高学生学习数学的兴趣,培养学生思维的灵活性和创造性。
学生在解题过程中思维是否灵活,有无创造性和概括能力,是反映其数学能力的一个重要标志,而能力的培养在于训练。训练可借助线段图来进行,利用线段图进行自编分数应用题训练、联想训练、利用线段图发现隐含关系的训练、一题多解的训练,以发展学生的创造性思维。
一、利用线段图进行自编题训练

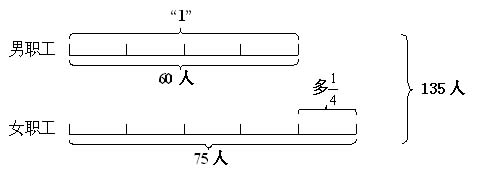
通过观察线段图,学生可以联想到:
①女职工有75人,男职工有60人,女职工是男职工的几倍?
②女职工有75人,男职工有60人,女职工比男职工多几分之几?
③男职工有60人,女职工比男职工多1/4,女职工有多少人?
④女职工有75人,比男职工多1/4,男职工有多少人?
……
学生编题的过程,就是对应用题数量关系和解题规律及有关基本概念进一步理解的过程,促使学生对分数三类应用题的内在联系有了更深的理解,进而掌握了解题规律,同时培养了思维的灵活性。
二、利用线段图进行联想训练
丰富的联想,能使学生的思维更加活跃,促使学生从多方面、多角度思考问题。联想是创造的前提,创造需要联想。联想训练,就是根据题目中一个或两个已知数量的含义,联想出一个或几个新的数量。学生可以通过已有的条件与问题,联想到接近、相似、相反或因果的条件和结果。联想实际上就是局部思维的发散,在发散的过程中,必须找到起控制作用的“核心”,也就是找到导致事物之间发生变化的原因。
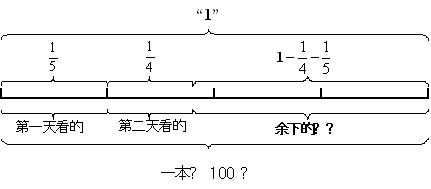
通过观察线段图,学生可以联想到:
①第一天看的页数:100×1/5=20(页)
②第二天看的页数:100×1/4=25(页)
③还剩的页数占全书的几分之几:1-1/5-1/4=11/20
④还剩下的页数:100×(1-1/5-1/4)=55(页)
在此基础上,还可以继续联想到:
①第一天看的页数是第二天看的几分之几? 20÷25=4/5
②第二天看的页数是第一天看的几倍?25÷20=5/4
③两天共看的占全书的几分之几?
45÷100=9/20
依据上述两次的联想,利用其联想结果,编出若干道分数应用题:
①一本书,我第一天看了总页数的1/5,第二天看了总页数的1/4,还剩下55页没看。这本书共多少页?
②一本书,我第一天看了总页数的1/5,第二天看了总页数的1/4,第二天比第一天多看5页。这本书共多少页?
……
学生通过一个直观简单的线段图进行联想和编题,不仅可以找到解题的途径和方法,而且通过发散可以进一步拓宽思路,促进思维的发展,培养思维的创造性。
三、利用线段图发现隐含关系的训练
在分数应用题中,一般都存在两种意义不同的量来表示同一个物体的大小(或多少),其中一个量,表示相当于单位“1”的几分之几,通常这个几分之几叫做“率”;另一个量,表示实际数量是多少。这两个量互相对应,所以一般把它们叫做对应数量(或者叫做量率对应),它们之间的关系叫做对应关系。量率对应关系是解答分数应用题的突破口,它贯穿于整个教学的全过程。分析清楚量率对应关系是解题最基本的方法之一。用线段图揭示对应关系,比较直观、形象。
例如:一辆汽车从甲地开往乙地,第一小时行了全程的1/4,第二小时行驶480千米,两小时共行驶了全程的5/8,甲、乙两地间的距离是多少千米?
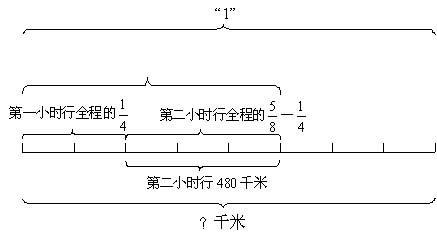
通过此图,我们可以找出几组对应关系:
①第一小时行驶的路程和1/4相对应;
②第二小时行驶的480千米和全程的(5/8-1/4)相对应;
③两小时共行驶的路程与5/8相对应;
④未行驶的路程与(1-5/8)相对应;
……
利用线段图,比较容易找出解答此题的关键是找到和“480千米”相对应的率,从而帮助学生找到解题途径,在分析问题与解决问题之间搭建了一座“桥梁”,促使学生能够灵活地解题。
对于较难的分数应用题,学生画出线段图,可把题中隐蔽、复杂的数量关系直观、清楚地展现出来。
例如:王师傅生产一批机器零件,第一天生产了全部的1/5多20个,第二天比第一天多生产1/2,还剩下30个未生产。这批零件共有多少个?
根据题意画线段图:
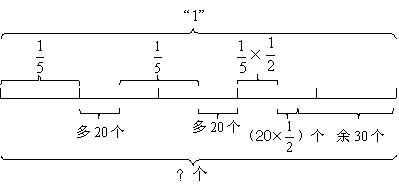
通过线段图,我们可以清楚地看到:(20+20+20×1/2+30)与(1-1/5-1/5-1/5×1/2) 相对应,解题方法自然找到了。这道题的数量关系较复杂,但是在画出线段图后,题中的数量关系就很清楚地显示出来了。
在分数应用题教学中,画线段图,可增强学生的学习情趣,同时在学生头脑中积累了丰富的表象,促其深入地理解量率的对应关系,为解决实际问题创造了条件。学生通过动手绘图的实际训练,既培养了实践操作能力,又发展了思维的灵活性和创造性。在时代呼唤创造性学习的今天,利用线段图解题,无疑是学生解答分数应用题的好帮手。教学中,只要我们少一点儿“匠气”,多一点儿“灵气”,就能用“教”的创新火种,引燃“学”的创新火焰,让学生在发挥创造性思维时享受学习的无限乐趣。